Clustering Shape Data
Contents
Title: Clustering High-Dimensional Landmark-Based Two-Dimensional Shape Data
Introduction
Shape analysis has been an important research topic with various applications in computer vision, object recognition, and medical imaging for last several decades. An important goal in shape analysis is to classify and recognize objects of interest according to the shapes of their boundaries. The majority of earlier work on shape analysis has focused on landmark-based analysis, where shapes are represented by a coarse, discrete sampling of the object contours.
Clustering landmark-based planar shape data raises four major challenges. First, planar shape data reside in a curved shape space, which is invariant under a similarity transformation including rigid rotation and translation, and nonrigid uniform scaling. Therefore, most clustering methods (e.g., K-means) proposed for Euclidean data cannot be used to cluster data in the curved shape space. Second, it is a standard high-dimensional-low-sample-size problem, since shape dimension, which is proportional to the number of landmark points, can be much larger than the sample size. Moreover, there may be significant amounts of noise in many of the landmark points, which is either associated with the complexity of the studied shapes or is caused by certain preprocessing steps such as image filtering and edge detection. Third, the landmark points along the boundaries of objects are inherently and spatially correlated with each other. Fourth, shape variation is commonly associated with some explanatory attributes (e.g., age, gender, or disease status). Ignoring such complex spatial correlation and explanatory attributes can introduce substantial errors in both clustering and classification results.
Questions
The aim of this project is to propose a mixture of offset-normal shape factor analyzer (MOSFA) model to address the four challenges.
Methods
We use the offset-normal shape distribution to characterize the variability of shape data in the curved shape space. To handle high dimensionality, we used a penalized clustering framework as an effective and powerful method to perform both variable selection and clustering. We integrated a latent factor analysis model to approximate the complex spatial correlation of shape data. We used a logistic regression model to build an association between mixing proportions and covariates of interest. We proposed an expectation-maximization (EM) algorithm and establish its convergence property. We established the asymptotic properties of penalized estimator obtained from the EM algorithm.
Findings
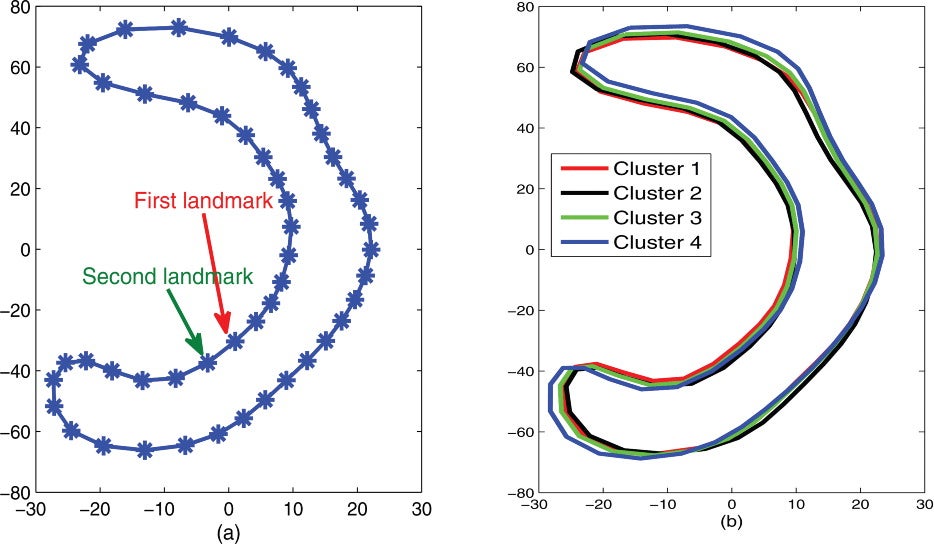
We applied the MOSFA model to the ADHD-200 CC shape dataset. Our clustering results remarkably reveal an intrinsic subpopulation structure in the mixed population with controls and subjects with ADHD. We calculated MPLE by using the EM algorithm and then the final MOSFA model was able to detect four clusters with 239, 98, 64, and 246 subjects, respectively. The first three clusters contain 391 normal controls and 10 ADHD patients, whereas the fourth cluster includes 13 normal controls and 233 ADHD patients. Thus, the first three clusters contain almost all the normal controls, whereas most diseased subjects fall into the last cluster. The mean shapes of the first three are similar to each other, whereas they are different from the mean shape of cluster four.
We are also interested in the estimated loading matrices for all the four clusters. The estimated number of factors in each cluster is 2. To extract the shape features of each cluster, we plotted each column in loading matrices for all the clusters. The columns of the loading matrices from the first three clusters have similar tendency, whereas they are different from those from the last cluster. It is consistent with the diagnosis information: most normal controls are in the first three clusters, whereas most ADHD patients are in the last cluster.
Then, we randomly chose subjects from each cluster and applied the ClosedCurves2D3D software (ClosedCurves2D3D) to compute a pair-wise geodesic path among the four clusters under the elastic Riemannian metric. It shows that the geodesic distance between subjects in the same cluster is smaller than that between subjects in different clusters. Furthermore, the geodesic distance between subjects in the first three clusters is much smaller than the geodesic distance between subjects in the first three clusters and those in the fourth cluster.


References
Huang, C., Styner, M., and Zhu, H.T. “Clustering High-Dimensional Landmark-based Two-dimensional Shape Data.”
Journal of the American Statistical Association, 110, 946-961, 2015.