Regression Models
Contents
Title: Regression models on Riemannian symmetric spaces
Introduction
Manifold-valued responses in curved spaces frequently arise in many disciplines including medical imaging, computational biology and computer vision, among many others. For instance, in medical and molecular imaging, it is interesting to delineate the changes in the shape and anatomy of a molecule. Regression anal- ysis is a fundamental statistical tool for relating a response variable to a covariate, such as age and gender. In particular, when both the response and the covariate(s) are in Euclidean space, the classical linear regression model and its variants have been widely used in various fields. However, when the response is in a Riemannian symmetric space (RSS) and the covariates are in Euclidean space, developing regression models for this type is difficult.
Questions
An intriguing question is whether there is a general regression framework for manifold-valued response in an RSS and covariates in a multi-dimensional Euclidean space. The aim of this paper is to give an affirmative answer to such a question.
Methods
- We propose an intrinsic regression model solely based on an intrinsic conditional moment for the response in an RSS, thus avoiding specifying any parametric distributions in a general RSS—the model can handle multiple covariates in Euclidean space.
- We develop several ‘efficient’ estimation methods for estimating the regression coefficients in this intrinsic model.
- We develop several test statistics for testing linear hypotheses of the regression coefficients.
- We develop a general asymptotic frame work for the estimates of the regression coefficients and test statistics.
- We systematically investigate the geometrical properties (e.g. chart invariance) of these parameter estimates and test statistics.
Findings
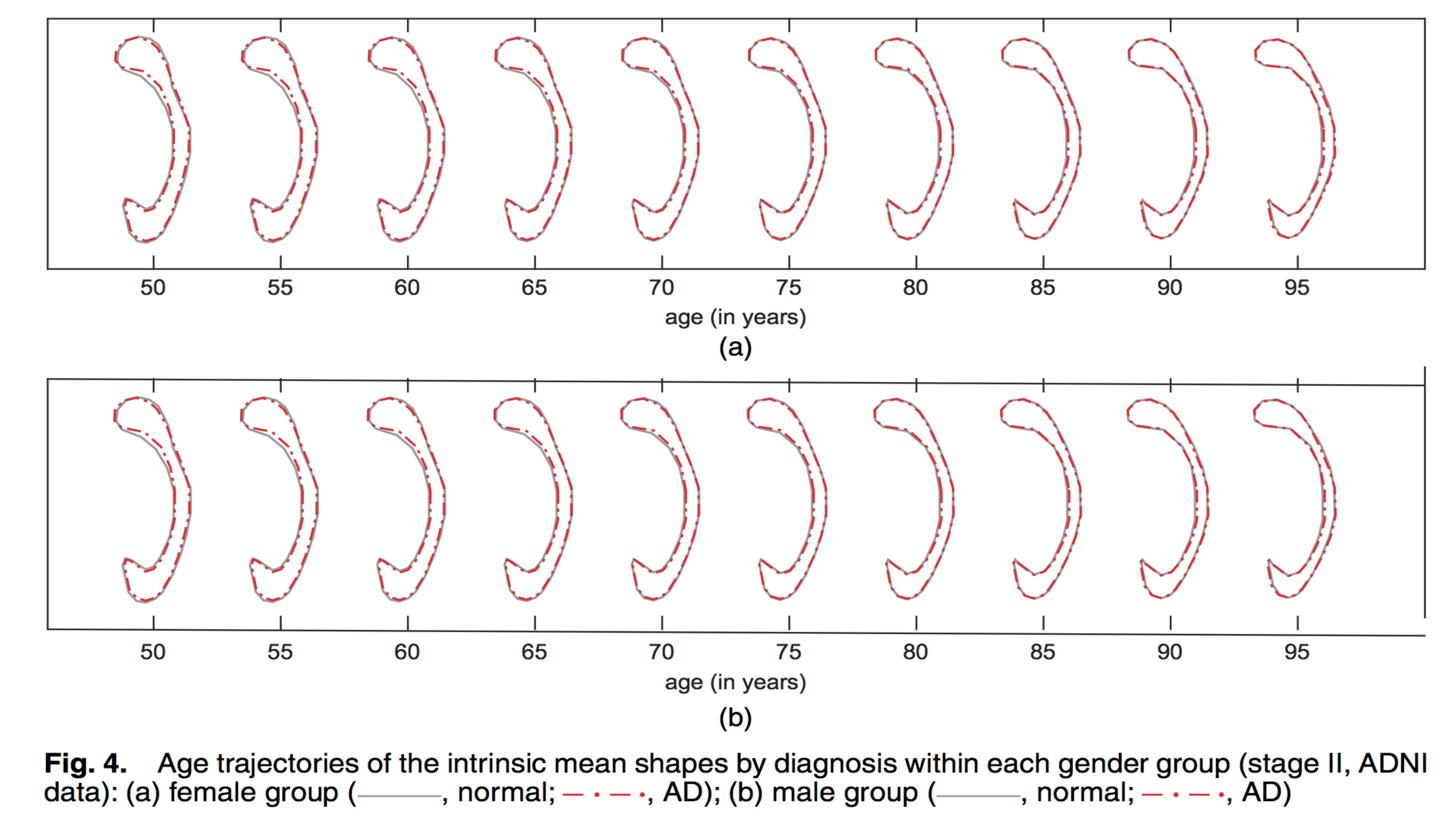
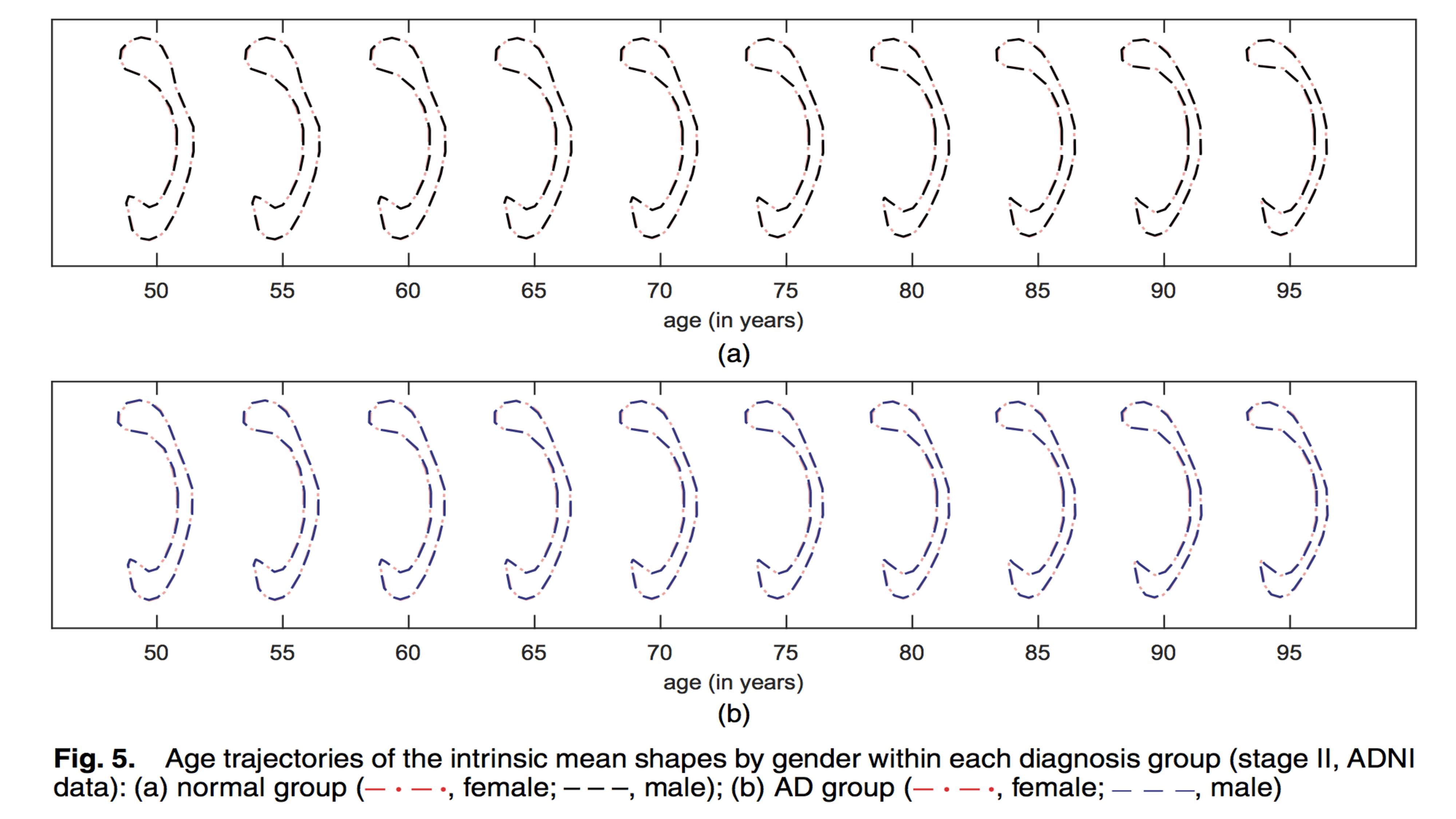
We are interested in characterizing the change of the CC contour shape as a function of three covariates including gender, age and AD diagnosis. We assessed whether there is an age×diagnosis interaction effect on the shape of the CC contour or not. The resting result indicates that there is a strong age-dependent diagnosis effect on the shape of the CC contours. It can be observed that there is a difference in shape along the inner side of the posterior splenium and isthmus subregions in both male and female groups. The splenium seems to be less rounded and the isthmus is thinner in subjects with AD than in healthy controls. We also assessed whether there is a gender effect on the shape of the CC contour or not. The Wald test was applied with its p-value 0.116. Thus, it is not significant at the 0:05 level of significance. It may indicate that there is no gender effect on the shape of the CC contours. Similar shapes of CC contours can be observed in males and females according to the mean age-dependent CC trajectories for the female and male groups within each diagnosis group.
References
Cornea, E., Zhu, H., Kim, P., Ibrahim, J. G. and the Alzheimer’s Disease Neuroimaging Initiative (2016),
Regression models on Riemannian symmetric spaces. J. R. Stat. Soc. B. doi:10.1111/rssb.12169